Concurso PMPR: gabarito extraoficial de Raciocínio Matemático

Pessoal, aqui é o Prof. Hugo Lima. Eu e o Prof. Arthur Lima resolvemos a prova da PMPR de Raciocínio Matemático. Aqui vocês vão ter acesso à nossa resolução da prova.

ASSISTA A CORREÇÃO DAS PROVAS NOS LINKS ABAIXO

Gabarito PMPR Raciocínio Matemático

UFPR – PMPR – 2021) No início do mês de julho, o valor de um produto sofreu um aumento de 10%. No início de agosto, o valor desse produto diminuiu 5% em relação ao mês anterior, fazendo com que ele passasse a custas R$ 250,80. Com base nos dados apresentados, o valor do produto antes do aumento ocorrido no início de julho era de:

A) 237

B) 238,26

C) 240

D) 245,8

E) 250,17

RESOLUÇÃO:

Inicialmente o produto valia x. Após o aumento de 10%, passou a valer x + 10%x = 1,1x. Após a redução de 5% passou a valer 1,1x – 5% 1,1x = 1,1x – 0,055x = 1,045x.

Esse valor corresponde a 250,80. Logo 1,045x = 250,80, ou seja, x = 250,80/1,045 = 240 reais.

RESPOSTA: C

UFPR – PMPR – 2021) Três torneiras estão despejando água continuamente. Após 1 minuto, o volume aproximado de água que sai da primeira é de 2,5 cm³, o da segunda é de 3 cm³ e o da terceira é de 4 mL. Quando a primeira torneira tiver despejado 1L, quantos litros a terceira torneira terá despejado a mais que a segunda?

A) 1,5 L

B) 1 L

C) 0,7L

D) 0,5L

E) 0,4L

RESOLUÇÃO:

Em 1 minuto, a primeira torneira despesa 2,5 cm³ de água. Para chegar em 1 litro, que corresponde a 1 dm³, serão necessários 1000/2,5 = 400 minutos.

Em 1 minuto, a segunda torneira despesa 3 cm³ de água. Já a terceira torneira despesa 4 mL = 4 cm³. Logo, a cada minuto a terceira torneira despeja 1 cm³ a mais que a segunda. Nesses 400 minutos, a terceira torneira despesa 400 cm³ = 0,4 dm³ = 0,4 L a mais que a segunda.

RESPOSTA: E

UFPR – PMPR – 2021) Em uma pesquisa sobre um determinado tipo de formiga, tomou-se um grupo desses insetos e mediu-se o comprimento de cada um deles. Os dados foram organizados como indica a tabela a seguir.

Sabendo que a média de comprimento dos insetos do grupo foi de 0,6 cm, qual é a quantidade de formigas cujo comprimento é de 0,8 cm?

A) 9

B) 8

C) 6

D) 4

E) 3

RESOLUÇÃO:

A média é dada por:

(0,2 x 1 + 0,3 x 3 + 0,4 x 4 + 0,5 x 4 + 0,6 x 3 + 0,7 x 4 + 0,8 x n + 0,9 x 1)/(1 + 3 + 4 + 4 + 3 + 4 + n + 1) = 0,6

(0,2 + 0,9 + 1,6 + 2 + 1,8 + 2,8 + 0,8 x n + 0,9)/(20 + n) = 0,6

(10,2 + 0,8 x n)/(20 + n) = 0,6

10,2 + 0,8 x n = 0,6n + 12

0,2n = 1,8

n = 9

RESPOSTA: A

UFPR – PMPR – 2021) Um irrigador distribui água numa região circular, de raio 13,5 m. Devido a um defeito, esse irrigador precisou ser trocado por outro, que passou a irrigar uma região circular de raio 18 m. Assinale a alternativa que representa a área da parte cinza, indicada na figura abaixo, que corresponde à região que passou a ser coberta pelo segundo irrigador, além daquela coberta pelo primeiro.

Use π = 22/7.

A) 346,50 m²

B) 396 m²

C) 409,5 m²

D) 445,4 m²

E) 495 m²

RESOLUÇÃO:

Basta fazer área = πR² – πr² = π (R² – r²) = π (18² – 13,5²) = 141,75π = 141,75 x 22/7 = 445,5 m².

RESPOSTA: D

UFPR – PMPR – 2021) Um hospital possui duas alas de UTI, totalizando 210 leitos. A primeira destina 25% dos leitos a pacientes infectados pela COVID-19; e a segunda, 50% dos leitos a pacientes com essa doença. Sabe-se que o número total de leitos destinados a pacientes com COVID-19, nas duas UTIs, representa 40% do total de leitos de UTI no hospital. Desse modo, o número de leitos destinados a esses pacientes, na UTI com menor capacidade, é:

A) 15

B) 21

C) 48

D) 63

E) 84

RESOLUÇÃO:

Total de leitos UTI: 210

Seja x a quantidade de leitos de UTI da primeira ala e y a quantidade de leitos de UTI da segunda ala.

25%x são destinados a COVID-19

50%y são destinados a COVID-19

Número total de leitos destinados a COVID-19 = 40% x 210 = 84 = 25%x + 50%y.

Lembrando ainda que x + y = 210 –> x = 210 – y

84 = 25%x + 50%y

84 = 0,25 (210 – y) + 0,5y

84 = 52,5 – 0,25y + 0,5y

84 = 52,5 + 0,25y

y = 126

x = 210 – 126 = 84.

A menor ala é a de 84 leitos, dos quais 25% são 21 leitos.

RESPOSTA: B

UFPR – PMPR – 2021) Considere a tabela e o gráfico que descrevem a capacidade de armazenamento de grãos de quatro cooperativas:

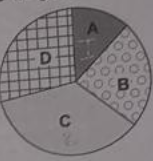
De acordo com o gráfico de setores, à direita da tabela, as regiões A, B, C e D correspondem respectivamente às seguintes cooperativas:

A) 2, 3, 4, 1

B) 4, 1, 2, 3

C) 2, 4, 3, 1

D) 1, 3, 4, 2

E) 1, 4, 2, 3

RESOLUÇÃO:

A maior região do gráfico é C, que corresponde a 304 toneladas – Cooperativa 2. Logo, nas alternativas de resposta podemos excluir A, C e D, visto que elas não possuem a cooperativa 2 associada ao setor C do gráfico.

A menor região do gráfico é A, que corresponde a 108 toneladas – Cooperativa 1. Perceba que apenas na alternativa E, dentre as que sobraram, temos a cooperativa 1 associada ao setor A do gráfico.

RESPOSTA: E

UFPR – PMPR – 2021) A figura abaixo ilustra um corrimão instalado numa rampa de acesso.

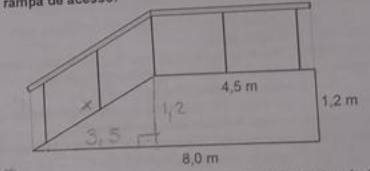
Com base nessa figura, o comprimento do corrimão é de:

A) 5,7 m

B) 6,9 m

C) 7,8 m

D) 8,2 m

E) 9 m

RESOLUÇÃO:

Temos um triângulo retângulo cujos catetos são 1,2 m e 8 – 4,5 = 3,5 m. Logo, isso nos dá uma hipotenusa de √(1,2² + 3,5²) = 3,7. Somado a 4,5, o corrimão mede 8,2 m.

RESPOSTA: D

UFPR – PMPR – 2021) Geraldo e Maurício possuem coleções de cartões postais de regiões do Paraná. A coleção de Geraldo pode ser organizada em um álbum, colocando-se 3 cartões por folha. usando o mesmo número de folhas, pode-se organizar a coleção de Maurício, colocando-se 5 cartões por folha. Além disso, se Maurício der 6 cartões de sua coleção a Geraldo, as coleções de ambos passarão a ter a mesma quantidade de cartões. Quantos cartões há nas coleções de Geraldo e Maurício juntas?

A) 48

B) 33

C) 27

D) 23

E) 14

RESOLUÇÃO:

Seja g a quantidade de cartões de Geraldo e m a de Maurício.

3 cartões por folha x número de folhas = g

5 cartões por folha x número de folhas = m

Isolando o número de folhas em cada relação acima, chegamos a:

m/5 = g/3

Além disso, m – 6 = g + 6 –> m = g + 12

(g + 12)/5 = g/3

3g + 36 = 5g

2g = 36

g = 18

m = 18 + 12 = 30

Assim, m + g = 30 + 18 = 48.

RESPOSTA: A

UFPR – PMPR – 2021) Uma região de plantio possui formato retangular. Ampliando seu lado menor em 8 m, obteve-se uma nova região retangular, conforme ilustra a figura ao lado. O perímetro da região ampliada passou a ser de 242 m, e sua área ficou 20% maior que a área da região inicial.

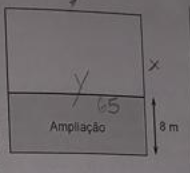
Com base nisso, o perímetro da região cinza, que corresponde à ampliação feita, é de:

A) 113 m

B) 146 m

C) 162 m

D) 210 m

E) 226 m

RESOLUÇÃO:

Sejam y e x os lados do retângulo inicial. O lado x foi aumentado em 8 metros. Logo, o perímetro é:

x + 8 + y + x + 8 + y = 242 –> 2x + 2y = 226 –> x + y = 113 m –> x = 113 – y

A área inicial era xy. A área final ampliada corresponde a 20% de xy. Logo:

8y = 20% xy

8y = 0,2y(113 – y)

8y = 22,6y – 0,2y²

8 = 22,6 – 0,2y

0,2y = 14,6

y = 73

Perímetro da ampliação: 73 + 73 + 8 + 8 = 162.

RESPOSTA: C

UFPR – PMPR – 2021) Em uma pesquisa sobre sobre a preferência pelos sabores laranja, maracujá ou uva, dos sucos comercializados por uma empresa, foram entrevistadas 70 pessoas, pedindo-se que cada uma delas manifestasse preferência por até 2 sabores. Sabe-se que 5 pessoas não quiseram participar da pesquisa; 19 escolheram apenas o sabor laranja; 12, apenas o sabor maracujá; 16, apenas o sabor uva; e 7, os sabores de maracujá e laranja. Dos entrevistados, quantos escolheram exatamente dois sabores, sendo um deles uva?

A) 9

B) 11

C) 12

D) 16

E) 18

RESOLUÇÃO:

Ao todo foram entrevistadas 70 pessoas. Retirando as 5 que não quiseram participar, restam 65. Retirando aquelas que escolheram apenas um sabor (19 – laranja; 12 – maracujá e 16 – uva) restam 65 – 19 – 12 – 16 = 18. Dessas 18, sabemos que 7 escolheram maracujá e laranja. Então restam 18 – 7 = 11. Essas 11 se referem justamente às pessoas que escolheram dois sabores sendo um deles uva, que são os locais assinalados por y e x na figura abaixo. Não temos ninguém na interseção dos três conjuntos já que na pesquisa a preferência era por até 2 sabores.

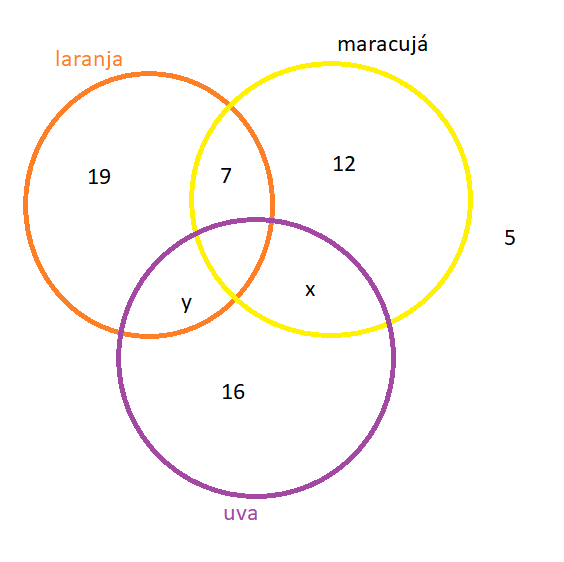
RESPOSTA: B

UFPR – PMPR – 2021) Uma primeira urna possui uma bola branca e duas pretas. Uma segunda urna possui duas bolas brancas e uma preta. Uma terceira urna, por sua vez, possui uma bola branca e uma preta. uma pessoa vendada retira uma bola da primeira urna e a coloca na segunda. Em seguida, retira uma bola da segunda urna e a coloca na terceira. Por fim, retira uma bola da terceira urna.

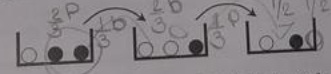
Sabendo que todas as bolas são idênticas em forma e peso, quantas possibilidades há de que a bola retirada da terceira urna seja preta?

A) 5

B) 8

C) 14

D) 15

E) 18

RESOLUÇÃO:

1º caso) retira-se uma preta da primeira urna (duas possibilidades de fazê-lo) e uma preta da segunda (duas possibilidades de fazê-lo). Agora a terceira urna tem duas bolas pretas. Com isso, temos duas possibilidades de retirar uma bola preta. Assim, o total nesse caso é 2 x 2 x 2 = 8.

2º caso) retira-se uma preta da primeira urna (duas possibilidades de fazê-lo) e uma branca da segunda (duas possibilidades de fazê-lo). Agora a terceira urna tem uma bola preta. Assim, o total nesse caso é 2 x 2 x 1 = 4.

3º caso) retira-se uma branca da primeira urna (uma possibilidade de fazê-lo) e uma preta da segunda (uma possibilidade de fazê-lo). Agora a terceira urna tem duas bolas pretas. Assim, o total nesse caso é 1 x 1 x 2 = 2.

4º caso) retira-se uma branca da primeira urna (uma possibilidade de fazê-lo) e uma branca da segunda (três possibilidades de fazê-lo). Agora a terceira urna tem uma bola preta. Assim, o total nesse caso é 1 x 3 x 1 = 3.

Total de possibilidades: 8 + 4 + 2 + 3 = 17.

RESPOSTA: Deve ser anulada

UFPR – PMPR – 2021) Um recipiente possui formato de um cubo de aresta 12 cm. Há no recipiente 0,944 L de água e, no fundo, um dado também de formato cúbico, com aresta medindo 2 cm. Se o dado for retirado do recipiente, a altura do líquido nesse recipiente será de aproximadamente:

A) 11,4 cm

B) 7 cm

C) 6,5 cm

D) 6 cm

E) 5,7 cm

RESOLUÇÃO:

O volume do dado é de 2³ = 8 cm³ = 8 mL = 0,008 L mas isso é desnecessário pra questão.

A altura de 0,944 L de água no recipiente cúbico de aresta igual a 12 cm é dada por:

12 x 12 x h = 944 –> h = 944/0,0144 = 6,555 cm

RESPOSTA: C

CONFIRA TAMBÉM O GABARITO DE INFORMÁTICA