Gabarito ISS Campinas – Matemática Financeira, Estatística e Raciocínio Lógico (Auditor)

Caros alunos, deixo a seguir o meu Gabarito ISS Campinas para as disciplinas de Matemática Financeira, Estatística e Raciocínio Lógico do cargo de Auditor Fiscal Tributário.

Conheça os cursos do Direção Concursos – videoaulas e PDFs completos e focados no seu concurso

GABARITO ISS CAMPINAS – MATEMÁTICA FINANCEIRA

VUNESP – ISS-CAMPINAS – 2019)

Nos três últimos anos, devido a uma crise de oferta de petróleo, a gasolina chegou a sofrer um aumento de 130%, em média, chegando ao patamar de R$ 4,90. Então, o preço da gasolina antes desse aumento era de

(A) R$ 2,00.

(B) R$ 1,60.

(C) R$ 1,75.

(D) R$ 1,45.

(E) R$ 2,13.

RESOLUÇÃO:

Sendo P o preço da gasolina antes do aumento, sabemos que:

Preço final = Preço antes do aumento x (1 + 130%)

4,90 = P x (1 + 1,30)

4,90 = P x (2,30)

P = 4,90 / 2,30

P = 49 / 23

P = 2,13 (aproximadamente)

Resposta: E

VUNESP – ISS-CAMPINAS – 2019)

Uma casa está alugada por R$ 1.550,00 mensais e um investidor pretende comprá-la, com a condição de que a taxa de retorno com o aluguel seja de pelo menos 0,9% a.m. Para atender essa condição, o máximo que ele deve pagar pela casa é, aproximadamente:

(A) R$ 170.000,00.

(B) R$ 200.000,00.

(C) R$ 190.000,00.

(D) R$ 180.000,00.

(E) R$ 210.000,00.

RESOLUÇÃO:

O investidor terá uma renda mensal perpétua de R = 1550 reais caso adquira a casa. A taxa de retorno é j = 0,9%am. Assim, o valor justo (VP) a ser pago pela casa é dado por:

R = VP x j

1550 = VP x 0,9%

VP = 1550 / 0,9%

VP = 1550 / (0,9/100)

VP = 1550 x 100 / 0,9

VP = 155000 / 0,9

VP = 172.222,22 reais

Resposta: A

VUNESP – ISS-CAMPINAS – 2019)

Um imóvel é ofertado pelo valor de R$ 150.000,00, e um comprador oferece pagar R$ 100.000,00 no ato da compra, mais cinco cheques pré-datados de R$ 10.000,00 cada um, o primeiro para 30 dias e os seguintes, nos próximos cinco meses, sem cobrar juros. O vendedor sabe que pode descontar os cheques em um banco a uma taxa de 5% ao mês em desconto comercial. Então, o desconto para pagamento à vista que o vendedor pode dar sobre o total do imóvel para que os capitais sejam equivalentes é de

(A) 7,5%.

(B) 5%.

(C) 10%.

(D) 12,5%.

(E) 15%.

RESOLUÇÃO:

Vejamos qual será o valor presente pago pelo comprador. Além dos 100.000 reais na data inicial, devemos trazer 5 prestações de valor P = 10.000 reais para a data inicial,

VP = 10000 x 0,2155 / 0,0608

VP = 2155 / 0,0608

VP = 35.444,08 reais

           Portanto, o valor presente a ser pago é de 100.000 + 35.444,08 = 135.444,08 reais. O desconto que pode ser dado é de 150.000 – 135.444,08 = 14.555,92 reais.

           Percentualmente, o desconto é de:

P = 14555,92 / 150000 = 0,097 = 9,7% (aproximadamente 10%)

OBS.: caso utilizemos desconto SIMPLES, o gabarito seria exato (5%). Entretanto, não vislumbro elementos no enunciado que remetam ao regime simples.

Resposta: D (ou B, se considerado o regime simples)

VUNESP – ISS-CAMPINAS – 2019)

A empresa A contrata a empresa B para prestação de um serviço cujo valor à vista é V. Pelo contrato, A vai pagar B no prazo de 2 anos e meio, em uma única parcela que incluirá o valor à vista mais juros contratuais de 10% ao ano. Se o contrato firmado entre as partes para a quitação da dívida prevê taxa de juros compostos com convenção linear, então o valor mais próximo do total de juros que B deve pagar a A ao quitar a dívida no prazo é de, aproximadamente:

(A) 0,25V.

(B) 0,20V.

(C) 0,27V.

(D) 0,30V.

(E) 2,50V.

RESOLUÇÃO:

Pela convenção linear, primeiro fazemos o cálculo do montante após t = 2 anos (parte inteira do prazo):

M₁ = C x (1 + j)^t

M₁ = V x (1 + 10%)²

M₁ = V x (1,10)²

M₁ = V x 1,21

           Em seguida, calculamos o montante final utilizando M₁ como capital inicial, na fórmula de juros simples, pelo prazo fracionário t = 0,5 ano:

M = C x (1 + j x t)

M = (V x 1,21) x (1 + 10% x 0,5)

M = (V x 1,21) x (1 + 5%)

M = V x 1,21 x 1,05

M = 1,2705 V

           Os juros a serem pagos são:

J = M – C

J = 1,2705V – V

J = 0,2705V

Resposta: C

VUNESP – ISS-CAMPINAS – 2019)

A empresa E desconta um título de valor nominal V em um banco que realiza essa operação aplicando taxa de desconto comercial simples (ou “por fora”, como essa modalidade de cobrança também é conhecida) de 2% ao mês. Se o prazo para apresentação do título é de 10 meses, então a taxa efetiva mensal de juros cobrada pelo banco nessa operação é de

(A) 3,5%.

(B) 4,0%.

(C) 3,0%.

(D) 2%.

(E) 2,5%.

RESOLUÇÃO:

Podemos relacionar a taxa por fora com a taxa por dentro (efetiva) no regime simples assim:

(1/j_f) – (1/j_d) = t

(1/0,02) – (1/j_d) = 10

50 – (1/j_d) = 10

50 – 10 = (1/j_d)

40 = (1/j_d)

j_d = 1/40

j_d = 0,025 = 2,5% am

Resposta: E

VUNESP – ISS-CAMPINAS – 2019)

O esquema a seguir representa o fluxo de caixa relativo à compra de um bem, realizada nas seguintes condições: uma primeira parcela de entrada no valor x reais na data 0 (zero) cujo valor foi de 20% do valor V do bem; uma segunda parcela de valor anotado na data 2, quitando totalmente o valor da compra. A taxa de juros contratada foi de 1% ao mês de juros compostos.

De acordo com os dados, um dos valores seguintes é o da entrada x:

(A) R$ 3.000,00.

(B) R$ 2.000,00.

(C) R$ 3.500,00.

(D) R$ 2.500,00.

(E) R$ 4.000,00.

RESOLUÇÃO:

Após pagar 20% do valor V do bem na data inicial, restou uma dívida de 80% do valor do bem, ou seja, 0,8V. Esta é a dívida inicial (C). Essa dívida cresceu a juros compostos de j = 1% ao mês pelo prazo de t = 2 meses, chegando ao montante de M = 10.201 reais. Assim, podemos escrever que:

M = C x (1 + j)^t

10201 = 0,8V x (1 + 1%)²

10201 = 0,8V x (1,01)²

10201 = 0,8V x 1,0201

10201 / 1,0201 = 0,8V

10000 = 0,8V

V = 10000 / 0,8

V = 12500 reais

           A entrada foi de 20% de V, ou seja, 0,20 x 12500 = 2500 reais.

Resposta: D

VUNESP – ISS-CAMPINAS – 2019)

Um banco faz um empréstimo de R$ 60.000,00 a uma empresa com prazo de 5 anos, e taxa de juros de 2% ao mês pelo sistema price. Ao calcular o valor da prestação mensal por uma calculadora financeira, foi obtido o valor de R$ 1.726,00. Em cada prestação, uma parte corresponde ao juro sobre a dívida e outra parte para amortização. Então, a soma das amortizações das duas primeiras parcelas é de, aproximadamente:

(A) R$ 1.060,00.

(B) R$ 2.390,00.

(C) R$ 2.230,00.

(D) R$ 5.160,00.

(E) R$ 1.000,00.

RESOLUÇÃO:

No primeiro mês temos juros de J₁ = 60000 x 2% = 1200 reais. Assim, a amortização na primeira parcela de 1726 reais é:

A₁ = P – J₁

A₁ = 1726 – 1200 = 526 reais

           Com isso, a dívida caiu para 60000 – 526 = 59474 reais, afinal somente a amortização reduz a dívida. No segundo mês, os juros foram de J₂ = 59474 x 2% = 1189,48 reais. E a amortização na segunda parcela foi:

A₂ = P – J₂

A₂ = 1726 – 1189,48 = 536,52 reais

           Logo, a amortização das duas primeiras parcelas soma 526 + 536,52 = 1062,52 reais.

Resposta: A

VUNESP – ISS-CAMPINAS – 2019)

Um banco faz um empréstimo de R$ 60.000,00 a uma empresa com prazo de 5 anos, e taxa de juros de 2% ao

mês pelo sistema SAC. Então, o valor da vigésima prestação mensal é de, aproximadamente:

(A) R$ 1.730,00.

(B) R$ 1.820,00.

(C) R$ 1.940,00.

(D) R$ 1.200,00.

(E) R$ 2.200,00.

RESOLUÇÃO:

Veja que 5 anos correspondem a 5 x 12 = 60 meses. A amortização mensal é de:

A = VP / n

A = 60000 / 60

A = 1000 reais

           Após 19 meses, o saldo devedor cai para 60000 – 19×1000 = 41000 reais. Assim, os juros do 20º período são:

J = 41000 x 2%

J = 820 reais

           Deste modo, a 20ª parcela é P = A + J = 1000 + 820 = 1820 reais.

Resposta: B

VUNESP – ISS-CAMPINAS – 2019)

Um empresário possui 4 duplicatas, vencíveis em 30, 60, 90 e 120 dias, nos valores de R$ 10.000,00, R$ 15.000,00, R$ 20.0000,00 e R$ 20.000,00, respectivamente. Ele pretende receber antecipadamente esses quatro valores pagando a taxa de desconto comercial de 5% ao mês. O Banco propõe a troca desses quatro títulos por um único título no valor de R$ 64.000,00 a vencer em certo prazo n. Então, para que seja indiferente ao empresário, ou seja, para que haja equivalência de capitais, à taxa de desconto comercial de 5% ao mês, este prazo n, deverá ser de, aproximadamente e arredondado para número inteiro:

(A) 55 dias.

(B) 50 dias.

(C) 65 dias.

(D) 75 dias.

(E) 35 dias.

RESOLUÇÃO:

O valor presente dos 4 títulos na data zero, pelo desconto comercial simples, é de:

VP = 10000.(1-5%.1) + 15000.(1-5%.2) + 20000.(1-5%.3) + 20000.(1-5%.4)

VP = 56000 reais

           Este também deve ser o valor presente do título de valor nominal 64000 reais na data “n” dias, ou seja, n/30 meses:

56000 = 64.000 . (1 – 5% . n/30)

56000 / 64000 = 1 – 5% . n/30

0,875 = 1 – 5% . n/30

5% . n/30 = 1 – 0,875

5% . n/30 = 0,125

5% . n = 3,75

n = 3,75 / 0,05

n = 75 dias

Obs.: embora a questão não tenha esclarecido se o regime era simples ou composto, usamos o regime simples para realizar o cálculo aproximado, em especial pelo fato de que as opções de resposta apresentavam prazos que, em meses, seriam fracionários. Além disso, estávamos buscando a variável que representa o prazo, que estaria no expoente, caso estivéssemos trabalhando no regime composto.

Resposta: D

VUNESP – ISS-CAMPINAS – 2019)

Um investidor aplicou R$ 50.000,00 por 4 meses a juros simples e à taxa de juros de 3% ao mês. Ao final do período, aplicou esse primeiro montante, agora a juros compostos e à mesma taxa de 3% a.m. por dois meses, obtendo esse segundo montante. Os juros da segunda operação é x vezes o juro obtido na primeira operação.

Então, o valor de x é igual a, aproximadamente:

(A) 0,48.

(B) 0,65.

(C) 0,62.

(D) 0,82.

(E) 0,56

RESOLUÇÃO:

Após o primeiro prazo, temos:

M₁ = C x (1 + j x t)

M₁ = 50000 x (1 + 0,03 x 4)

M₁ = 50000 x (1 + 0,12)

M₁ = 50000 x (1,12)

M₁ = 56000 reais

           Após o segundo prazo:

M₂ =  C x (1 + j)^t

M₂ = 56000 x (1 + 0,03)²

M₂ = 56000 x (1,03)²

M₂ = 56000 x 1,0609

M₂ = 59410,40 reais

           Assim, os juros da primeira operação são:

J₁ = 56000 – 50000 = 6000 reais

           E os juros da segunda operação são:

J₂ = 59410,40 – 56000 = 3410,40 reais

           Dividindo os juros das duas operações, temos:

3410,40 / 6000 =

0,5684

Resposta: E

Conheça os cursos do Direção Concursos em PDF e vídeo

GABARITO ISS CAMPINAS – ESTATÍSTICA

VUNESP – ISS-CAMPINAS – 2019)

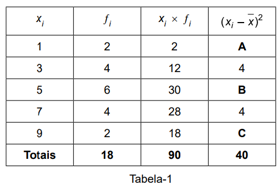
A tabela-1 de distribuição de frequência mostra a organização e síntese de 18 dados x_i colhidos como amostra para um estudo estatístico, onde a coluna ƒ_i é a que registra os valores das frequências, enquanto a coluna contém os valores dos quadrados dos desvios.

Os valores substituídos pelas letras A, B e C na tabela são, respectivamente:

(A) 0, 16, 0.

(B) 4, 4, 4.

(C) 16, 0, 16.

(D) 0, 4, 0.

(E) 16, 4, 16.

RESOLUÇÃO:

A média é dada pela divisão entre a soma dos dados (coluna x_i  . f_i), que é 90, pelo total de frequências f_i, que é 18. Ou seja,

Média = 90 / 18 = 5

           Este é o valor de “x barra”. Portanto, temos:

A = (1 – 5)² = 16

B = (5 – 5)² = 0

C = (9 – 5)² = 16

Resposta: C

VUNESP – ISS-CAMPINAS – 2019)

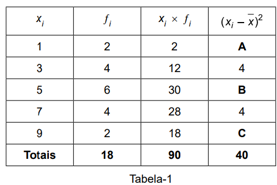
A tabela-1 de distribuição de frequência mostra a organização e síntese de 18 dados xi colhidos como amostra para um estudo estatístico, onde a coluna ƒi é a que registra os valores das frequências, enquanto a coluna contém os valores dos quadrados dos desvios.

Entre os números a seguir, o que mais se aproxima da variância amostral é:

(A) 5.

(B) 3.

(C) 1.

(D) 7.

(E) 9.

RESOLUÇÃO:

Precisamos criar a coluna em que multiplicamos as frequências pelos quadrados dos desvios:

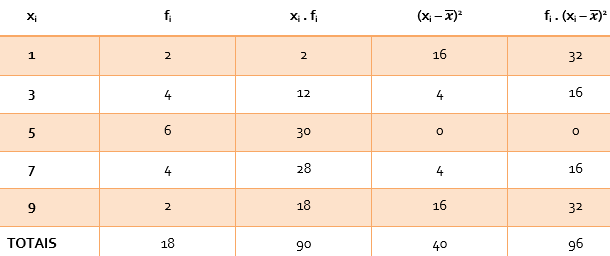
           Assim, a variância é dada por:

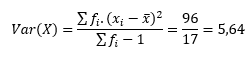
Resposta: A

VUNESP – ISS-CAMPINAS – 2019)

Sabe-se que as probabilidades de um carro transportar 1, 2, 3, 4 ou 5 pessoas são de 0,05, 0,20, 0,40, 0,25 e 0,10, respectivamente. Se em uma cidade chegaram 400 carros, a estimativa de pessoas que chegaram é de

(A) 1600.

(B) 1260.

(C) 1400.

(D) 1320.

(E) 2000.

RESOLUÇÃO:

O valor esperado do número de pessoas em um carro é dado pela soma das quantidades de pessoas (x) multiplicadas pelas suas probabilidades p(x). Ou seja,

E(X) = 1.0,05 + 2.0,20 + 3.0,4 + 4.0,25 + 5.0,10

E(X) = 0,05 + 0,4 + 1,2 + 1 + 0,5

E(X) = 3,15

           Portanto, espera-se 3,15 pessoas por carro, em média. Como são 400 carros, devemos ter um total de 3,15 x 400 = 1260 pessoas.

Resposta: B

VUNESP – ISS-CAMPINAS – 2019)

Ao operar em um turno de trabalho, uma linha de produção se interrompe totalmente se uma máquina M1 falhar. Para diminuir o risco de interrupção, ligou-se ao sistema uma máquina M2 programada para entrar imediatamente em funcionamento caso M1 falhe, fazendo com que o sistema prossiga. A probabilidade de M1 falhar é de 1/20 e a probabilidade de M2 falhar é também de 1/20. A probabilidade de que o sistema não se interrompa durante um turno de trabalho após a inclusão de M2 é de

(A) 99,75%.

(B) 95%.

(C) 99%.

(D) 90,25%.

(E) 97,5%.

RESOLUÇÃO:

A probabilidade de interrupção é dada pela probabilidade de as duas máquinas falharem simultaneamente, isto é, P = 1/20 x 1/20 = 1/400 = 0,0025 = 0,25%.

Portanto, a probabilidade de o sistema NÃO se interromper é de 100% – 0,25% = 99,75%.

Resposta: A

VUNESP – ISS-CAMPINAS – 2019)

De uma população, escolheu-se uma amostra casual de 10 pessoas e os seus pesos Y, em quilogramas, e alturas X, em centímetros, foram anotados. Sabendo-se que a equação de regressão linear correspondente é igual a Yc = 36,8 + 0,16x, então o peso esperado de uma pessoa que tenha 180 cm de altura, em quilos, é aproximadamente igual a

(A) 70,3.

(B) 61,2.

(C) 63,2.

(D) 52,6.

(E) 65,6.

RESOLUÇÃO:

Uma pessoa com x = 180cm deve ter um peso de aproximadamente:

Yc = 36,8 + 0,16x

Yc = 36,8 + 0,16 . 180

Yc = 65,6 kg

Resposta: E

RACIOCÍNIO LÓGICO

VUNESP – ISS-CAMPINAS – 2019)

Considere falsidades as duas proposições a seguir:

I. Ana concorre ao cargo de auditora fiscal ou Jorge concorre ao cargo de professor.

II. Se Carlos está fazendo a prova, então ele está concorrendo ao cargo de auditor fiscal.

Com base nas informações apresentadas, assinale a alternativa que contém uma proposição necessariamente

verdadeira.

(A) Ana não concorre ao cargo de auditora fiscal e Carlos concorre ao cargo de professor.

(B) Carlos não está fazendo a prova e Jorge não concorre ao cargo de professor.

(C) Carlos está fazendo a prova ou Jorge concorre ao cargo de professor.

(D) Ana concorre ao cargo de professora e Jorge concorre ao cargo de auditor fiscal.

(E) Carlos concorre ao cargo de auditor fiscal ou Ana concorre ao cargo de professor.

RESOLUÇÃO:

           Como as proposições são falsas, suas NEGAÇÕES são verdadeiras:

I. Ana NÃO concorre ao cargo de auditora fiscal E Jorge NÃO concorre ao cargo de professor

II. Carlos ESTÁ fazendo a prova E ele NÃO está concorrendo ao cargo de auditor fiscal

           Sabendo que as frases acima são verdadeiras, e vendo que elas são conjunções, podemos garantir que cada parte é verdadeira. Ou seja:

– Ana não concorre ao cargo de auditora fiscal

– Jorge não concorre ao cargo de professor

– Carlos está fazendo a prova

– Carlos não está concorrendo ao cargo de auditor fiscal

           Portanto, a alternativa C é uma disjunção verdadeira, pois  a sua primeira parte (Carlos está fazendo a prova) é V.

Resposta: C

VUNESP – ISS-CAMPINAS – 2019)

Pretende-se analisar se uma proposição P, composta por quatro proposições simples, implica uma proposição Q, composta pelas mesmas quatro proposições simples, combinadas com conectivos distintos. Como são desconhecidos os valores lógicos das proposições simples envolvidas, pretende-se utilizar uma tabela verdade, estudando-se todas as possíveis combinações entre os valores lógicos dessas proposições, a fim de ser utilizada a definição de implicação lógica. Dessa forma, o referido número total de combinações possíveis é

(A) 64.

(B) 8.

(C) 4.

(D) 32.

(E) 16.

RESOLUÇÃO:

           Temos 4 proposições simples, o que leva a uma tabela com 2⁴ = 16 linhas. Este é o número de combinações possíveis.

Resposta: E

VUNESP – ISS-CAMPINAS – 2019)

Considere as seguintes proposições:

I. Se Marcos é auditor fiscal ou Luana é administradora, então Marcos é auditor fiscal e Luana é administradora.

II. Se Marcos é auditor fiscal e Luana é administradora, então Marcos é auditor fiscal se, e somente se, Luana

é administradora.

As proposições I e II, nessa ordem, são classificadas como

(A) contingência e contradição.

(B) contingência e contingência.

(C) contradição e tautologia.

(D) contingência e tautologia.

(E) tautologia e tautologia.

RESOLUÇÃO:

A primeira frase é uma contingência. Ela pode ser V, caso seja verdade que Marcos é auditor e Luana é administradora. E ela pode ser F, caso apenas uma das coisas seja verdade (por exemplo, se Marcos for Auditor mas Luana não for administradora, teremos VàF).

A segunda frase é uma tautologia. Caso seja verdade que Marcos é auditor e Luana é administradora, a primeira parte da condicional fica V. E, com isso, automaticamente a segunda parte da condicional (que é uma bicondicional) fica V também, de modo que não teremos VàF em nenhuma hipótese.

Resposta: D

VUNESP – ISS-CAMPINAS – 2019)

Uma proposição logicamente equivalente à afirmação

“Se Marcos é engenheiro, então Roberta é enfermeira e Ana é psicóloga” é apresentada na alternativa:

(A) Se Roberta não é enfermeira ou Ana não é psicóloga, então Marcos não é engenheiro.

(B) Ana é psicóloga, Marcos é engenheiro e Roberta é enfermeira.

(C) Se Marcos não é engenheiro, então Roberta não é enfermeira e Ana não é psicóloga.

(D) Se Roberta é enfermeira e Ana é psicóloga, então Marcos é engenheiro.

(E) Roberta não é enfermeira, Ana não é psicóloga e Marcos não é engenheiro.

RESOLUÇÃO:

           Sabemos que pàq equivale à sua contrapositiva ~qà~p. Negando as duas proposições e trocando-as de lugar, temos a contrapositiva:

“Se Roberta NÃO é enfermeira OU Ana NÃO é psicóloga, então Marcos NÃO é engenheiro”

           Temos isso na alternativa A.

Resposta: A

VUNESP – ISS-CAMPINAS – 2019)

Considere verdadeiras as seguintes premissas:

I. Ou Carlos é auditor fiscal ou Vânia é auditora fiscal.

II. Se Carlos é auditor fiscal, então Roberto é juiz.

III. Roberto é juiz ou Vânia é auditora fiscal.

Das alternativas a seguir, a única que contém uma afirmação que pode ser tomada como conclusão para se

ter, juntamente com as três premissas apresentadas, um argumento válido é:

(A) Carlos e Vânia não são auditores fiscais e Roberto é juiz.

(B) Carlos e Vânia são auditores fiscais e Roberto é juiz.

(C) Carlos não é auditor fiscal, Vânia é auditora fiscal, e Roberto não é juiz.

(D) Carlos e Vânia não são auditores fiscais e Roberto não é juiz.

(E) Carlos é auditor fiscal, Vânia não é auditora fiscal e Roberto não é juiz.

RESOLUÇÃO:

           Analisando as opções de resposta, veja que as letras A, B e D não podem ser gabarito. Isto porque elas deixam a premissa I falsa, pois se trata de uma disjunção exclusiva, onde os valores lógicos de Carlos e Vânia devem ser opostos.

           A letra E também não pode ser gabarito, pois nela a proposição II ficaria falsa (V–>F). Assim, o gabarito só pode ser a alternativa C que, para ser verdadeira, obriga as 3 premissas a serem verdadeiras.

Resposta: C

Conheça os cursos completos do Direção Concursos