Gabarito ISS Manaus – Estatística, Matemática e Raciocínio Lógico – prova resolvida

Caros alunos,

Vejam a minha resolução das questões de estatística, matemática e raciocínio lógico do concurso de Auditor do ISS Manaus.

MATEMÁTICA E RACIOCÍNIO LÓGICO

FCC – ISS/Manaus – 2019) Se 3 painéis solares fotovoltaicos produzem 70 kWh de energia em 50 dias, o número de painéis solares que produzem 112 kWh de energia em 15 dias é (A) 13. (B) 12. (C) 15. (D) 14. (E) 16.

RESOLUÇÃO:

Veja que temos um “produto” (energia produzida) que, para ser gerado, exige dois “ingredientes” (painéis e dias). Podemos escrever assim:

Painéis Dias Energia

3 50 70

P 15 112

Podemos multiplicar os ingredientes de uma linha pelo produto da outra, e igualar tudo, ficando com:

3x50x112 = Px15x70

3x5x112 = Px15x7

112 = Px7

P = 112/7 = 16 painéis

Resposta: E

FCC – ISS/Manaus – 2019) Uma repartição pública analisou metade de um lote de processos ao ritmo de 40 processos por dia e, com a equipe de funcionários reforçada, a outra metade a um ritmo de 360 processos por dia. O ritmo médio de análise dos processos constantes desse lote foi de (A) 72 processos por dia. (B) 96 processos por dia. (C) 200 processos por dia. (D) 100 processos por dia. (E) 84 processos por dia.

RESOLUÇÃO:

Sejam 2P processos. Neste caso, metade (P) foi analisada ao ritmo de 40 processos por dia, gastando um total de dias igual a:

Dias para a primeira parte = P / 40

A outra metade (P) foi analisada ao ritmo de 360 processos por dia, gastando um total de dias igual a:

Dias para a segunda parte = P / 360

Portanto, o tempo total gasto foi de:

Dias = P/40 + P/360 = 9P/40 + P/360 = 10P/360 = P/36

Veja que foram analisados 2P processos em P/36 dias, resultado em uma média de:

Ritmo médio = processos / dias

Ritmo médio = 2P / (P/36) = 2P x 36/P = 2 x 36 = 72 processos por dia

Resposta: A

• Saiba mais: Concursos Sefaz: confira a situação de todos os estados

FCC – ISS/Manaus – 2019) Sérgio recebeu um adiantamento e negociou que a devolução seria paga em duas parcelas iguais de R$ 1.210,00, a primeira, um mês após o recebimento do adiantamento, e a segunda, um mês depois do pagamento da primeira parcela. Sabendo que foram cobrados juros compostos de 10% ao mês, o valor que Sérgio recebeu pelo adiantamento foi de (A) R$ 2.210,00. (B) R$ 2.420,00. (C) R$ 2.010,00. (D) R$ 2.100,00. (E) R$ 2.200,00.

RESOLUÇÃO:

Trazendo as duas parcelas de 1210 para o valor presente, usando a taxa de 10%am, temos:

VP = 1210/(1+10%) + 1210/(1+10%)²

VP = 1210/1,10 + 1210 / 1,21

VP = 1100 + 1000

VP= 2100 reais

Resposta: D

FCC – ISS/Manaus – 2019) Para José, uma caixa de ferramentas é boa se, e somente se, para todo parafuso que houver na caixa, houver, também, uma chave que encaixa nele. Assim, se uma caixa de ferramentas não é boa para José, então, nela: (A) existe pelo menos um parafuso que encaixa em todas as chaves. (B) existe pelo menos uma chave que não encaixa em nenhum parafuso. (C) nenhum parafuso encaixa em todas as chaves. (D) existe pelo menos um parafuso que não encaixa em nenhuma chave. (E) para cada parafuso, existe pelo menos uma chave que não encaixa nele.

RESOLUÇÃO:

Temos a proposição:

caixa boa <==> há uma chave para todo parafuso

Trata-se de uma bicondicional. Para tratar de uma caixa que NÃO é boa, a primeira parte da bicondicional será F. Assim, a segunda parte também precisa ser F. Ou seja, é preciso haver algum parafuso para o qual não há chave.

Por isso, podemos marcar a alternativa D.

Resposta: D

FCC – ISS/Manaus – 2019) Há sete cidades, chamadas A, B, C, D, E, F e G, ao longo de uma estrada que corre em direção norte-sul. Essas cidades se localizam uma em relação a outra de acordo com os seguintes dados: − Há exatamente 3 cidades ao sul de A. − D está ao norte de F, mas não é a cidade mais ao norte de todas, e F não é a cidade mais ao sul de todas. − A primeira cidade ao norte de C é E. − Dentre as cidades que se encontram entre D e C está B. − Não há cidades entre F e E. Então, (A) F está ao sul de A. (B) não há cidades entre G e B. (C) G é a cidade mais ao sul de todas. (D) E está ao norte de A. (E) não há cidades entre D e F.

RESOLUÇÃO:

Podemos representar o sul à esquerda e o norte à direita. Assim, sabendo que há 3 cidades ao sul de A, podemos colocar assim:

__ __ __ A __ __ __

A primeira cidade ao norte de C é E. Temos algo assim:

… C E …

Não há cidades entre F e E. Como ao sul de E está C, precisamos que F esteja ao norte de E, ficando:

… C E F …

D está ao norte de F. Como D não é a cidade mais ao norte, e F não é a cidade mais ao sul, temos algo assim:

…C E F … D …

Perceba que não dá para colocar essas 4 cidades ao norte de A. Portanto, é preciso que C, E e F estejam ao sul de A:

C E F A __ __ __

Veja que as vagas ao norte devem ser ocupadas por B, D, G. D não pode ser a cidade mais ao norte, de modo que a posição mais ao norte deve ser ocupada por B ou G. Veja ainda que B precisa estar entre D e C, de modo que não pode também ser a cidade mais ao norte. A cidade mais ao norte só pode ser G:

C E F A __ __ G

Como entre D e C temos a cidade B, só há uma posição possível para D e B:

C E F A B D G

Pela ordenação acima, vemos que F está ao sul de A.

Resposta: A

• Saiba mais: Concurso Sefaz CE: edital este ano para 100 vagas

ESTATÍSTICA

FCC – ISS/Manaus – 2019) De um estudo, obtiveram-se informações de uma amostra aleatória extraída de uma população. Em um teste de hipóteses, foram formuladas as hipóteses H₀ (hipótese nula) e H₁ (hipótese alternativa) para analisar um parâmetro da população com base nos dados da amostra. O nível de significância deste teste corresponde à probabilidade de

(A) rejeitar H0, independente de H0 ser falsa ou verdadeira.

(B) não rejeitar H0, dado que H0 é falsa.

(C) rejeitar H0, dado que H0 é falsa.

(D) rejeitar H0, dado que H0 é verdadeira.

(E) não rejeitar H0, independente de H0 ser falsa ou verdadeira.

RESOLUÇÃO:

               Questão teórica sobre teste de hipóteses! Basta lembrar que o nível de significância corresponde à probabilidade de incorrermos no erro do tipo I, ou seja, quando a hipótese nula é VERDADEIRA mas, ainda assim, a REJEITAMOS (quando o correto seria aceitá-la). Temos isso na alternativa D.

Resposta: D

FCC – ISS/Manaus – 2019) Conforme um levantamento realizado em um órgão público e analisando a distribuição dos salários, em R$ 1.000,00, de todos os seus funcionários, obteve-se a tabela de frequências absolutas abaixo, com k sendo um número inteiro positivo.

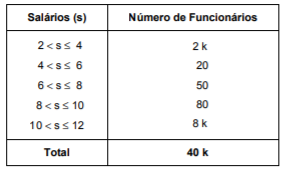
Considere que a média aritmética (Me) foi calculada considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo, que a mediana (Md) foi calculada pelo método da interpolação linear e que a moda (Mo) foi obtida pela relação de Pearson, ou seja, Mo = 3 Md − 2 Me. O valor encontrado para Mo, em R$ 1.000,00, foi igual a

(A) 1,82 k.

(B) 1,76 k.

(C) 1,70 k.

(D) 1,64 k.

(E) 1,60 k.

RESOLUÇÃO:

               Podemos começar observando que o total de funcionários é:

40k = 2k + 20 + 50 + 80 + 8k

40k = 10k + 150

30k = 150

k = 5

               Assim, temos a tabela de frequências abaixo, onde substituí o valor de k. Aproveitei para já calcular os pontos médios dos salários:

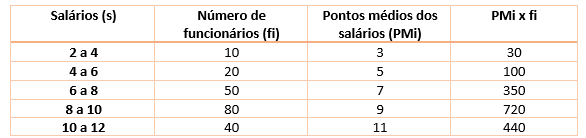
               Veja que a soma da coluna PMi x fi é igual a 1640. Assim, como a soma das frequências é 40k = 40.5 = 200, a média é dada por:

Média = Somatório de PMi x fi / Frequências

Média = 1640 / 200

Média = 8,2

               Para obter a mediana, podemos começar colocando a coluna das frequências acumuladas:

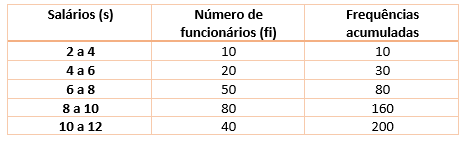
               Veja que temos n = 200 frequências, de modo que a mediana está na posição n/2 = 100. Esta posição está na classe de 8 a 10 salários. Afinal, esta classe começa com 80 frequências acumuladas e termina em 160. Podemos, portanto, montar a nossa interpolação linear:

                              80         100                      160

Frequências        |————|——————|

Salários               |————|——————|

                              8               Md                   10

               Montando a proporção:

(100 – 80) / (160 – 80) = (Md – 8) / (10 – 8)

20/80 = (Md – 8) / 2

20/40 = (Md – 8)

0,5 = Md – 8

Md = 8,5

               Assim, a moda de Pearson é:

Mo = 3 Md − 2 Me

Mo = 3.8,5 – 2.8,2

Mo = 9,1

               Dividindo por k = 5, temos:

9,1 / 5 = 1,82

               Logo, Mo = 9,1 = 1,82.5 = 1,82k.

Resposta: A

FCC – ISS/Manaus – 2019) Em uma empresa, o número de empregados que são mulheres está para o número de empregados que são homens assim como 2 está para 3. Decide-se extrair uma amostra aleatória de 4 empregados desta empresa, com reposição. A probabilidade de que nesta amostra haja no máximo 2 homens é de

(A) 47,52%.

(B) 50,00%.

(C) 49,92%.

(D) 60,00%.

(E) 52,48%.

RESOLUÇÃO:

               Como as mulheres estão para os homens assim como 2 está para 3, podemos dizer que, a cada 5 empregados, 2 são mulheres e 3 são homens. Assim, a probabilidade de retirar uma mulher é de 2/5, e a probabilidade de retirar um homem é de 3/5.

               Como queremos ter NO MÁXIMO 2 homens, podemos calcular a probabilidade de termos 0, 1 ou 2 homens. Para tanto, podemos considerar uma distribuição binomial na qual “sucesso” é retirar um homem, com um total de n = 4 tentativas, sendo p = 3/5 = 0,6 a probabilidade de sucesso.

               Lembrando que, na distribuição binomial:

P(k sucessos) = C(n,k).p^k.(1-p)^n-k

Logo,

P(0) + P(1) + P(2) =

C(4,0).0,6⁰.0,4⁴ + C(4,1).0,6¹.0,4³ + C(4,2).0,6².0,4² =

1.1.0,0256 + 4.0,6.0,064 + 6.0,36.0,16 =

0,5248 =

52,48%

Resposta: E

FCC – ISS/Manaus – 2019) Uma grande população formada pelos comprimentos de  determinadas peças é normalmente distribuída com média μ igual a 20 centímetros. Observa-se que 84% das peças da população possuem um comprimento inferior a 25 centímetros.

Se 90% das peças possuem um comprimento superior a x centímetros, então, x é igual a

(A) 14,7.

(B) 12,2.

(C) 13,6.

(D) 11,8.

(E) 15,8.

RESOLUÇÃO:

               O enunciado nos informa que, para esta distribuição, P(X<25) = 0,84. Devemos buscar um valor “z” tal que P(Z<z) = 0,84 também. Para isto, como P (Z<0) = 0,5, podemos dizer que P(0<Z<z) deve ser igual a 0,84 – 0,5 = 0,34.

               Observando na tabela, vemos que P(0<Z<1) = 0,34. Logo, X = 25 deve corresponder a Z = 1. Na transformação Z:

Z = (X – média)/(desvio padrão)

1 = (25 – 20)/(desvio padrão)

desvio padrão = 5

               Agora queremos um valor z tal que P(Z > z) = 0,9. Para tanto, P(Z < z) = 0,1.

               Veja que P(0<Z<1,28) = 0,4 na tabela. Portanto, P(Z<1,28) = 0,4, e P(Z > 1,28) = 0,1. Pela simetria da curva normal, podemos dizer que P(Z < -1,28) = 0,1 também.

               Assim, fica claro que devemos usar z = -1,28.

Z = (X – média)/(desvio padrão)

-1,28 = (X – 20)/5

-5 x 1,28 = X – 20

-6,4 = X – 20

X = 13,6 cm

Resposta: C

• Saiba mais: Concurso Receita Federal 2019: visão COMPLETA do edital

FCC – ISS/Manaus – 2019) Analisando as vendas trimestrais realizadas pela empresa Gama no período de 2016 a 2018, obteve-se a equação da tendência utilizando o método dos mínimos quadrados com base nestas 12 observações, ou seja, X_t = 10 + 1,5t, em que X corresponde às vendas trimestrais (em milhões de reais) e t = 1 representa o primeiro trimestre de 2016, t = 2 representa o segundo trimestre de 2016 e assim por diante.

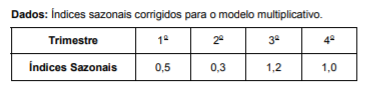
A previsão das vendas para o segundo trimestre de 2020, levando em conta o movimento sazonal do período e considerando o modelo multiplicativo, é igual, em milhões de reais, a

(A) 11,5.

(B) 11,8.

(C) 11,1.

(D) 12,6.

(E) 12,0.

RESOLUÇÃO:

               O segundo trimestre de 2020 seria t = 18. Neste caso, temos:

X_t = 10 + 1,5t

X₁₈ = 10 + 1,5.18

X₁₈ = 37

               Aplicando o multiplicador de sazonalidade para o 2º semestre (0,3), ficamos com

X₁₈ = 37 x 0,3 = 11,1

Resposta: C

Saudações,

Prof. Arthur Lima