
Veja neste artigo o meu gabarito SEFAZ DF para o cargo de Auditor Fiscal. Vamos resolver as questões da prova de Matemática Financeira, Estatística e Raciocínio Lógico aplicada hoje pela banca Cebraspe/Cespe.
Veja a correção das demais disciplinas em:
GABARITO SEFAZ DF DIREÇÃO CONCURSOS
Minha impressão geral sobre a prova:
Gabarito SEFAZ DF Matemática Financeira
Em determinada loja, uma bicicleta é vendida por R$1.720 à vista ou em duas vezes, com entrada de R$920 e uma parcela de R$920 com vencimento para o mês seguinte. Caso queira antecipar o crédito correspondente ao valor da parcela, o lojista paga para a financeira uma taxa de antecipação correspondente a 5% do valor da parcela.
Cespe – SEFAZ DF – 2020) Na compra a prazo, o custo efetivo da operação de financiamento pago pelo cliente será inferior a 14% ao mês.
RESOLUÇÃO:
A dívida ao sair da loja é de 1720 – 920 = 800 reais. Após 1 mês será preciso pagar 920 reais, o que implica em juros de 120 reais. Percentualmente, esses juros representam 120/800 = 0,15 = 15% ao mês. Item ERRADO
Gabarito: E
Cespe – SEFAZ DF – 2020) No caso de uma venda a prazo em que o lojista optasse pela antecipação do crédito correspondente à parcela que só seria paga no mês seguinte, o valor total que ele receberia (entrada mais antecipação) seria superior a R$1.790.
RESOLUÇÃO:
Ao antecipar em 1 mês a parcela de 920 reais, com taxa de 5%, temos o valor presente:
VP = 920 / (1+5%) = 920 / 1,05 = 876,19 reais
Assim, o total recebido seria a soma da primeira parcela (920) e a antecipação da segunda (876,19), totalizando R$1.796,19. Item CERTO.
Gabarito: C
Cespe – SEFAZ DF – 2020) Considere que um comprador sabe que o preço da bicicleta não irá aumentar durante 1 mês e tem a possibilidade de investir suas economias em uma aplicação com rendimento líquido de 5% ao mês. Nessa situação, o comprador poderá realizar a compra à vista da bicicleta investindo nessa aplicação uma quantia inferior a R$1.650, independentemente de o regime de capitalização da aplicação ser simples ou composto.
RESOLUÇÃO:
Se eu aplicar 1650 reais por 1 mês a uma taxa de 5%, terei, ao final do período, o montante:
M = 1650 x (1 + 5%) = 1650 x 1,05 = 1732,50 reais
Veja que isto é MAIS do que eu preciso para comprar a bicicleta à vista (1720). Portanto, realmente eu posso investir uma quantia INFERIOR a 1650 reais por um mês e, após isso, efetuar a compra à vista da bicicleta. Item CERTO.
Gabarito: C
Gabarito SEFAZ DF Estatística – prova resolvida
A partir de uma amostra aleatória simples de tamanho n, sabe-se que a média de uma variável X foi igual a 3. Considerando que os valores possíveis para a variável X sejam -1 e +4, julgue os itens que se seguem.
Cespe – SEFAZ DF – 2020) Nesta amostra aleatória, a quantidade de observações iguais a +4 foi igual a 0,8n.
RESOLUÇÃO:
Vamos testar a afirmação deste item. Suponha que 0,8n observações foram iguais a +4. Neste caso, o restante (0,2n) são observações iguais a -1. A média seria dada por:
Média = Soma / quantidade
A soma total dos n valores seria:
Soma = 0,8n.(+4) + 0,2n.(-1)
Soma = 3,2n – 0,2n = 3n
A média seria, portanto,
Média = Soma / quantidade
Média = 3n / n
Média = 3.
De fato a média seria igual a 3, como previsto no enunciado. Esta é a única possibilidade de que a média atinja este valor, motivo pelo qual o item está CERTO.
Gabarito: C
Cespe – SEFAZ DF – 2020) O desvio padrão amostral da variável X foi igual ou superior a 2.
RESOLUÇÃO:
Já sabemos que 0,8n observações são iguais a +4 e que 0,2n observações são iguais a -1. Para facilitar, vamos imaginar que temos n = 10 observações, sendo 8 iguais a +4 e 2 iguais a -1.
Para calcular o desvio padrão, começamos pela variância. Vejamos:
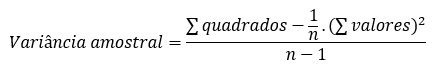
A soma dos quadrados dos valores é:
Soma quadrados = 8. 42 + 2.(-1)2 = 130
Soma valores = 8.4 + 2.(-1) = 30
Assim,
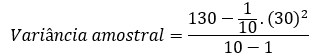
Variância amostral = 40/9 = 4,44
Logo, o desvio padrão amostral será a raiz de 4,44, que certamente é maior do que 2. Item CERTO
Gabarito: C
Cespe – SEFAZ DF – 2020) A mediana amostral da variável X foi igual a 2,5.
RESOLUÇÃO:
Vamos trabalhar novamente com o caso em que temos 10 valores, sendo dois iguais a -1 e oito iguais a +4. Neste caso, a mediana será igual a +4, pois tanto o quinto como o sexto termos desta distribuição, em ordem crescente, serão iguais a +4.
Item ERRADO.
Gabarito: E
Cespe – SEFAZ DF – 2020) A distribuição da variável X é simétrica em torno de sua média amostral.
RESOLUÇÃO:
Veja que a distribuição tem média 3, sendo oito valores iguais a 4 e dois valores iguais a -1. Esta distribuição, claramente, NÃO é simétrica em torno de sua média.
Item ERRADO.
Gabarito: E
Gabarito SEFAZ DF Raciocínio Lógico – prova resolvida
Considerando a proposição P: “Se o servidor gosta do que faz, então o cidadão-cliente fica satisfeito”, julgue os itens a seguir.
Cespe – SEFAZ DF – 2020) A proposição “O servidor não gosta do que faz, ou o cidadão-cliente não fica satisfeito” é uma maneira correta de negar a proposição P.
RESOLUÇÃO:
A proposição P é uma condicional p–>q, que é negada pela conjunção p e ~q. Assim, o conectivo esperado para a negação é o E, e não o OU, como aparece neste item. Item claramente ERRADO.
Gabarito: E
Cespe – SEFAZ DF – 2020) A proposição P é logicamente equivalente à seguinte proposição: “Se o cidadão-cliente não fica satisfeito, então o servidor não gosta do que faz”.
RESOLUÇÃO:
Se chamarmos de p o trecho “o servidor gosta do que faz” e de q o trecho “o cidadão-cliente fica satisfeito”, podemos dizer que a proposição P é dada por p–>q.
E a proposição deste item seria ~q –> ~p.
Sabemos que essas duas proposições são equivalentes. Trata-se da equivalência MANJADA que estava no nosso material de dicas finais:
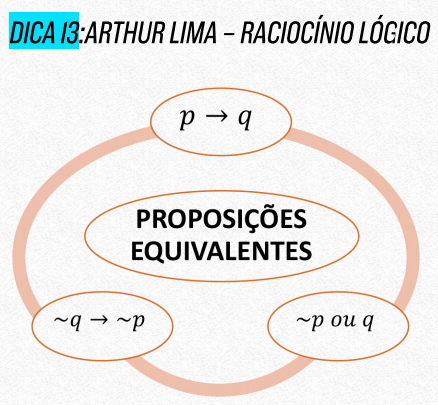
Item CERTO.
Gabarito: C
Cespe – SEFAZ DF – 2020) P é uma proposição composta formada por duas proposições simples, de modo que sua tabela-verdade possui 2 linhas.
RESOLUÇÃO:
ERRADO. Se temos 2 proposições simples, o número de linhas da tabela-verdade é dado por 2^2 = 4.
Gabarito: E
Veja a correção das demais disciplinas em: