
Pessoal, aqui é o Prof. Hugo Lima. Resolvi a prova do concurso do SERPRO de Raciocínio Lógico e Estatística para Especialização: Ciência de Dados. Aqui vocês vão ter acesso à resolução da prova.
Gabarito SERPRO Raciocínio Lógico
- CEBRASPE – SERPRO – 2021)
Julgue os itens seguintes, relativos a raciocínio lógico.
( ) Suponha que seja válida a seguinte proposição: P: Se Aldo não tem um número de CPF, então ele não pode viajar nem pode abrir uma empresa. Nessa situação, se Aldo pode abrir uma empresa, então ele já obteve o seu número de CPF.
( ) A negação da afirmação “Todos os amigos de Bianca são naturais de São Paulo” é: “Nenhum amigo de Bianca é natural de São Paulo”.
RESOLUÇÃO:
( ) Suponha que seja válida a seguinte proposição: P: Se Aldo não tem um número de CPF, então ele não pode viajar nem pode abrir uma empresa. Nessa situação, se Aldo pode abrir uma empresa, então ele já obteve o seu número de CPF.
Sabemos que uma condicional p –> q é equivalente a outra do tipo ~q –> ~p. Obtendo a equivalente da proposição P, temos:
Se Aldo pode viajar ou abrir uma empresa, então ele tem um número de CPF.
Perceba que “se Aldo pode abrir uma empresa” então será satisfeita uma das condições da disjunção: “Se Aldo pode viajar ou abrir uma empresa”. Satisfeita uma dessas condições, a disjunção passa a ser verdadeira. Assim, esse antecedente leva, logicamente, ao consequente, que é: ele tem um número de CPF.
Item correto.
( ) A negação da afirmação “Todos os amigos de Bianca são naturais de São Paulo” é: “Nenhum amigo de Bianca é natural de São Paulo”.
Item errado. A negação de todos é obtida com “algum”. Ou seja, basta que algum amigo de Bianca não seja natural de São Paulo para negar a afirmação.
Gabarito: CE
- CEBRASPE – SERPRO – 2021)
Suponha que sejam gerados 5 números válidos de CPF para serem atribuídos a 5 indivíduos distintos. Com base nessas informações, julgue os itens seguintes.
( ) A quantidade de formas de se fazer a atribuição desses CPFs a esses indivíduos é maior que 100.
( ) Suponha que, logo após a atribuição dos CPFs aos indivíduos, são escolhidos aleatoriamente 2 desses CPFs e separados 3 desses indivíduos. Nessa situação, a probabilidade de pelo menos um dos CPFs escolhidos pertencer a um dos indivíduos separados é igual a 3/5.
( ) Suponha que a seja o último dígito de um dos CPFs gerados, que b seja o último dígito de outro desses CPFs e que a e b sejam números ímpares consecutivos. Nessa situação, a + b é múltiplo de 4.
RESOLUÇÃO:
( ) A quantidade de formas de se fazer a atribuição desses CPFs a esses indivíduos é maior que 100.
Para o primeiro indivíduo temos 5 opções de CPF. Para o segundo, temos 4 opções. E assim em diante. Temos um caso de permuta, ou seja, a ordem importa, visto que os indivíduos e CPFs são distintos. Assim, a quantidade é de 5! = 5 x 4 x 3 x 2 x 1 = 120.
Item correto.
( ) Suponha que, logo após a atribuição dos CPFs aos indivíduos, são escolhidos aleatoriamente 2 desses CPFs e separados 3 desses indivíduos. Nessa situação, a probabilidade de pelo menos um dos CPFs escolhidos pertencer a um dos indivíduos separados é igual a 3/5.
De quantas formas consigo separar 3 indivíduos dentre 5 disponíveis? C(5, 3) = 5x4x3/3x2x1 = 10. Para ficar mais claro, vamos supor que os indivíduos sejam A, B, C, D e E. Assim, os trios possíveis de formar são:
ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE.
Suponha que os dois CPFs escolhidos aleatoriamente sejam os de A e B. Perceba que, dos 10 trios possíveis, somente no último (CDE) não temos a presença de A ou B. Nos outros 9 temos A ou B presentes. Ou seja, a probabilidade de pelo menos um dos CPFs escolhidos pertencer a um dos indivíduos separados é igual a 9/10.
Item errado.
( ) Suponha que a seja o último dígito de um dos CPFs gerados, que b seja o último dígito de outro desses CPFs e que a e b sejam números ímpares consecutivos. Nessa situação, a + b é múltiplo de 4.
Basta verificarmos se a soma de todos os ímpares consecutivos de 1 a 9 é múltiplo de 4.
1 + 3 = 4 –> é múltiplo de 4
3 + 5 = 8 –> é múltiplo de 4
5 + 7 = 12 –> é múltiplo de 4
7 + 9 = 16 –> é múltiplo de 4
Esses são todos os casos possíveis e, em todos eles, a + b é múltiplo de 4. Portanto, item correto.
Gabarito: CEC
Gabarito SERPRO Estatística
- CEBRASPE – SERPRO – 2021)
Considerando que o número X de erros registrados em determinado tipo de código computacional siga uma distribuição binomial com média igual a 4 e variância igual a 3, julgue os itens subsecutivos.
( ) É impossível haver registros de 18 erros nesse tipo de código computacional.
( ) A quantidade padronizada 𝑍 = (𝑋−4) / √3 segue distribuição normal padrão.
( ) A mediana de X é igual a 4.
( ) P(X = 0) = 3/4.
( ) O coeficiente de variação da distribuição de erros X é igual a 3.
RESOLUÇÃO:
( ) É impossível haver registros de 18 erros nesse tipo de código computacional.
Para resolver esse exercício, devemos lembrar que numa distribuição binominal:
E(x) = n . p
4 = n . p
Var(x) = n . p . (1-p)
3 = 4 . (1-p)
1 – p = ¾
p = ¼
4 = n . p
4 = n . ¼
n = 16
Assim, a probabilidade de se obter exatamente k sucessos em n tentativas:
Portanto, como n = 16, qualquer número de tentativas superior a 16 implica em n-k negativo. Portanto, é impossível haver registros de 18 erros nesse tipo de código computacional.
( ) A quantidade padronizada 𝑍 = (𝑋−4) / √3 segue distribuição normal padrão.
Item errado. A padronização aplicada nesse item serve para transformar uma distribuição normal qualquer em uma distribuição normal padrão. Aplicá-la ao nosso caso, em que temos uma distribuição binomial, não nos levará a uma distribuição normal padrão.
( ) A mediana de X é igual a 4.
Item correto. Na distribuição binomial a mediana também é dada por n.p, ou seja, é igual à média (valor esperado).
( ) P(X = 0) = 3/4.
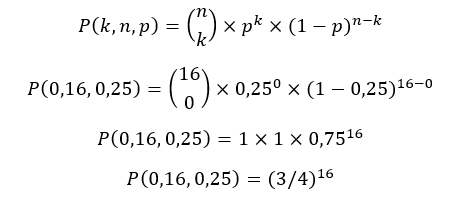
Item errado.
( ) O coeficiente de variação da distribuição de erros X é igual a 3.
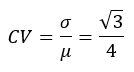
Item errado.
Gabarito: CECEE