Domine matemática financeira com 10 questões comentadas da banca Cesgranrio

Se você está se preparando para um concurso público com cobrança de matemática financeira, é importante saber que a Fundação Cesgranrio, organizadora do novo concurso Caixa, tem se destacado como uma das principais bancas na área bancária.

Pensando nisso, o professor Arthur Lima resolveu 5 questões recentes da banca sobre juros compostos.

Aproveite a oportunidade para revisar os principais conceitos, compreender o estilo da banca examinadora e reforçar seus conhecimentos!

1 – CESGRANRIO – BASA – 2018

Um valor inicial C0  foi capitalizado por meio da incidência de juros compostos mensais constantes iguais a 6,09%. Ao final de 6 meses, isto é, após 6 incidências dos juros, gerou-se o montante M. A partir do valor inicial C0, seria alcançado o mesmo montante M ao final de 12 meses (12 incidências), se os juros compostos mensais constantes tivessem sido iguais a

(A) 3,045%

(B) 3,000%

(C) 1,045%

(D) 1,450%

(E) 3,450%

Comentário:

No primeiro caso, temos prazo de t = 6 meses, e taxa de j = 6,09% ao mês. Assim,

M = C x (1+j)ᵗ

M = C₀ x (1+6,09%)⁶

M = C₀ x (1,0609)⁶

No segundo caso, temos prazo de t = 12 meses. Neste caso, para termos o mesmo capital e mesmo montante:

M = C₀ x (1 + j)¹²

Igualando as duas expressões do montante:

C0₀x (1,0609)⁶ = C₀ x (1 + j)¹²

(1,0609)⁶ = (1 + j)¹²

Tirando a raiz de 6º grau dos dois lados, temos:

1,0609 = (1+j)²

1,03² = (1+j)²

1,03 = 1 + j

j = 0,03 = 3% am

Gabarito: B

2 – CESGRANRIO – PETROBRÁS – 2018

Um equipamento, que poderia ser comprado por 100 milhões de reais à vista, foi financiado por meio de dois pagamentos semestrais sucessivos. O primeiro, no valor de 55 milhões de reais, foi pago seis meses após a compra; o segundo, no valor de 60,5 milhões de reais, foi pago 12 meses após a compra. O valor mais próximo da taxa anual equivalente cobrada nesse financiamento é igual a

(A) 15,5%

(B) 16,1%

(C) 20,0%

(D) 21,0%

(E) 22,5%

Comentário:

Sendo j a taxa de juros do financiamento, temos que:

Valor à vista do bem = soma dos valores presentes das prestações

100 = 55/(1+j) + 60,5/(1+j)²

Multiplicando todos os termos por (1+j)², temos:

100.(1+j)² = 55.(1+j) + 60,5

100.(1+2j+j²) = 55 + 55j + 60,5

100 + 200j + 100j² = 55 + 55j + 60,5

100j² + 145j -15,5 = 0

Aqui nós podemos resolver a equação de segundo grau ou testar as alternativas de resposta. Resolvendo a equação:

delta = 145² – 4.100.(-15,5) = 27225

raiz de delta = 165

Logo,

j = (-145 + 165)/(2.100) = 0,10 = 10% ao semestre

 Podemos obter a taxa anual equivalente lembrando que em teq = 1 ano temos t = 2 semestres. Logo,

(1 + 10%)² – 1 = jeq

jeq = 0,21 = 21% ao ano

Gabarito: D

3 – CESGRANRIO – ANP – 2016 

Por 3 anos seguidos, a taxa de inflação de certo país foi de 5% ao ano. Nesse período, o aluguel de um imóvel foi reajustado, anualmente, pelo índice de inflação, o que fez com que tal aluguel passasse a ser de p unidades monetárias. Para saber o valor do mesmo aluguel antes desses reajustes, basta dividir p por 

(A) 4,50 

(B) 1,50 

(C) 1,05 

(D) (1,50)³ 

(E) (1,05)³

Comentário:

Seja A o valor inicial do aluguel, antes dos reajustes. Cada aumento de 5% corresponde a multiplicar este valor por (1 + 5%), ou seja, por 1,05. Devemos fazer isso 3 vezes seguidas para chegar no preço final “p”, ou seja,

p = A x 1,05 x 1,05 x 1,05

p = A x 1,05³

A = p / 1,05³

Portanto, para chegar no valor inicial do aluguel (A), basta dividir o preço final p por 1,05³.

Gabarito: E

4 – CESGRANRIO – Banco do Brasil – 2015

Um cliente fez um investimento de 50 mil reais em um Banco, no regime de juros compostos. Após seis meses, ele resgatou 20 mil reais, deixando o restante aplicado. Após um ano do início da operação, resgatou 36 mil reais, zerando sua posição no investimento. A taxa semestral de juros proporcionada por esse investimento pertence a que intervalo abaixo?  Dado: √76 = 8,7

(A) 7,40% a 7,89% 

(B) 8,40% a 8,89% 

(C) 6,40% a 6,89%

(D) 6,90% a 7,39%

(E) 7,90% a 8,39%

Comentário:

Sendo j a taxa de juros semestral, podemos dizer que após 1 semestre o 

montante era:

M = C x (1 + j)ᵗ

M = 50.000 x (1 + j)¹

M = 50.000 x (1 + j)

Neste momento, foram retirados 20.000 reais, sobrando:

50.000 x (1+j) – 20.000

Este foi o capital aplicado por mais 1 semestre (até completar o ano), chegando ao montante final de 36.000 reais (que, ao ser resgatado, zerou o investimento). Ou seja:

M = C x (1 + j)ᵗ

36.000 = [50.000 x (1+j) – 20.000 ] x (1+j)¹

36.000 = [50.000 + 50.000j – 20.000 ] x (1+j)

36.000 = [30.000 + 50.000j ] x (1+j)

36.000 = 30.000 + 50.000j + 30.000j + 50.000j²

3,6 = 3 + 5j + 3j + 5j²

3,6 = 3 + 8j + 5j²

5j² + 8j – 0,6 = 0

delta = (-8)² – 4 x 5 x (-0,6) = 64 + 12 = 76

Portanto,

√delta = √76 = 8,7 = –> dado no enunciado

j = [ -(8) ± 8,7 ] / (2×5)

O valor positivo da taxa de juros é dado por:

j = [ -(8) + 8,7 ] / (2×5)

j  = 0,7 / 10 = 0,07

j = 7% ao semestre

Gabarito: D

5 – CESGRANRIO – Banco do Brasil – 2015

Um investimento rende à taxa de juros compostos de 12% ao ano com capitalização trimestral. Para obter um rendimento de R$ 609,00 daqui a 6 meses, deve-se investir, hoje, em reais,

(A) 6.460

(B) 10.000

(C) 3.138

(D) 4.852

(E) 7.271

Comentário:

A taxa nominal de 12% ao ano com capitalização trimestral corresponde à taxa efetiva de 12% / 4 = 3% ao trimestre (pois temos 4 trimestres em um ano). 

Assim, ficamos com:

M = C x (1 + j)ᵗ

C + 609 = C x (1 + 3%)²

C + 609 = C x (1,03)²

C + 609 = C x (1,0609)

609 = C x (1,0609) – C

609 = C x (1,0609) – 1 x C

609 = C x (1,0609 – 1)

609 = C x 0,0609

609 / 0,0609 = C

10.000 = C

Gabarito: B

6 – CESGRANRIO – BANCO DO BRASIL – 2015

Uma conta de R$ 1.000,00 foi paga com atraso de 2 meses e 10 dias. Considere o mês comercial, isto é, com 30 dias; considere, também, que foi adotado o regime de capitalização composta para cobrar juros relativos aos 2 meses, e que, em seguida, aplicou-se o regime de capitalização simples para cobrar juros relativos aos 10 dias.

Se a taxa de juros é de 3% ao mês, o juro cobrado foi de

(A) R$ 64,08

(B) R$ 79,17

(C) R$ 40,30

(D) R$ 71,51

(E) R$ 61,96

Comentário:

Para os 2 meses onde houve capitalização composta, temos:

M = C x (1+j)ᵗ

M = 1.000 x (1+3%)2

M = 1.000 x (1,03)²

M = 1.000 x 1,0609

M = 1.060,90 reais

Este valor é capitalizado, pelo regime simples, pelos 10 dias restantes, ou seja, 10/30 = 1/3 de mês. Logo,

Mfinal = 1.060,90 x (1+3% x 1/3)

Mfinal = 1.060,90 x (1+1%)

Mfinal = 1.060,90 x (1,01)

Mfinal = 1.071,51 reais

Assim, os juros totalizam 1.071,51 – 1.000 = 71,51 reais.

Gabarito: D

7 – CESGRANRIO – BASA/AM – 2015 

Aplicaram-se  R$ 2.000,00 em um fundo de investimento, por um ano, que rende à taxa bruta de 18% ao ano. O imposto de renda é de 22,5% sobre o ganho nominal. Em um ano em que a inflação foi de 7,5%, a taxa real de juros anual obtida nesse investimento foi de:

(A) 5,5%

(B) 6,5%

(C) 5,0%

(D) 4,5%

(E) 6,0%

Comentário:

O rendimento bruto é de 18% no ano. Como é pago 22,5% deste rendimento a título de imposto, sobra 100% – 22,5% = 77,5% do rendimento, ou seja, 77,5% x 18% = 13,95%. Este é o ganho aparente. Como a inflação foi de 7,5% neste mesmo período, podemos obter a taxa real lembrando que:

(1 + taxa real) = (1 + taxa aparente) / (1 + inflação)

(1 + taxa real) = (1 + 13,95%) / (1 + 7,5%)

(1 + taxa real) = (1,1395) / (1,075)

(1 + taxa real) = 1,06

taxa real = 0,06 = 6%

Gabarito: E

8 – CESGRANRIO – BASA – 2015

Um financiamento está sendo negociado a uma taxa nominal de 20% ao ano.

A taxa de juros efetiva anual desse financiamento, se os juros são capitalizados semestralmente, é:

  a) 12,10%

  b) 20,21%

  c) 21,00%

  d) 22,10%

  e) 24,20%

Comentário:

Se a capitalização é semestral, e temos 2 semestres em um ano, a taxa de juros efetiva é de 20% / 2 = 10% ao semestre. Calculando a taxa anual equivalente a 10%a.s., temos:

(1 + j)ᵗ = (1 + jeq)ᵗᵉ

(1 + 10%)ᵗ = (1 + jeq)ᵗᵉ

Como teq = 1 ano corresponde a t = 2 semestres, ficamos com:

(1 + 10%)² = (1 + jeq)¹

(1,10)² = 1 + jeq

1,21 = 1 + jeq

0,21 = jeq

21% ao ano = jeq

Gabarito: C

9 – CESGRANRIO – LIQUIGÁS – 2015

Um investimento em imóveis rende nominalmente 54,1% em 6 meses.

Se o investidor espera obter um ganho real de, no mínimo, 5% ao mês, qual deve ser o valor máximo da variação de preços no semestre?

  a) 15%

  b) 20%

  c) 24%

  d) 30%

  e) 34%

Comentário:

Temos um ganho aparente de jn = 54,1%. Um ganho real de 5%am corresponde, em um semestre (6 meses), a:

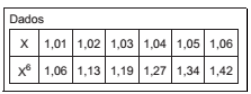
(1 + 5%)⁶ – 1 =

(1,05)⁶ – 1 =

1,34 – 1 =

0,34 =

34%

Veja, portanto, que o ganho real é de jreal = 34% no semestre. Podemos obter a inflação lembrando que:

1+jreal = (1+jn) / (1+i)

1+0,34 = (1+0,541) / (1+i)

1,34 = 1,541 / (1+i)

1+i = 1,541 / 1,34

1+i = 1,15

i = 0,15 = 15%

A variação de preços (inflação) no semestre deve ser de até 15%.

Gabarito: A

10 – CESGRANRIO – Banco do Brasil – 2015

A empresa ALFA tomou um empréstimo no valor de 100 mil reais, em janeiro de 2015, a uma taxa de juros de 12% ao ano, no regime de juros compostos, a serem pagos em 3 parcelas anuais, consecutivas e postecipadas. A primeira parcela, a ser paga em janeiro de 2016, corresponderá a 20% do valor do empréstimo; a segunda parcela, um ano após a primeira, será igual a 30% do valor do empréstimo, e a terceira parcela a ser paga, em janeiro de 2018, liquidará a dívida. A quantia, em milhares de reais, que mais se aproxima do valor da terceira parcela é igual a

(A) 72,0

(B) 90,5

(C) 56,0

(D) 64,2

(E) 81,8

Comentário:

Após 1 ano, a dívida terá chegado ao valor de:

Dívida após 1 ano = 100.000 + 12%x100.000 = 112.000 reais

O primeiro pagamento é de 20% do valor inicial da dívida:

20% x 100.000 = 20.000 reais.

Assim, a dívida cai para:

Dívida após primeiro pagamento = 112.000 – 20.000 = 92.000 reais

Durante o segundo ano, essa dívida cresce mais 12%, chegando a:

Dívida após 2 anos = 92.000 + 12% x 92.000 = 103.040 reais

A segunda prestação é de 30% do valor inicial da dívida, isto é, 30.000 reais. Assim, a dívida cai para:

Dívida após o segundo pagamento = 103.040 – 30.000 = 73.040 reais

Ao longo do terceiro ano esta dívida cresce mais 12%:

Dívida após 3 anos = 73.040 + 12% x 73.040 = 81.804,80 reais

Este é o valor que deve ser pago para a dívida ser quitada.

Gabarito: E